Fie datele de intrare:
n=3 posturi.
P1(x1,y1)=(2,2), P2(x2,y2)=(6,2), P3(x3,y3)=(4,4)
L=10 si H=5
La iesire o sa avem poligoanele ca in imagine cu ariile:15.5; 25,5 si 9.
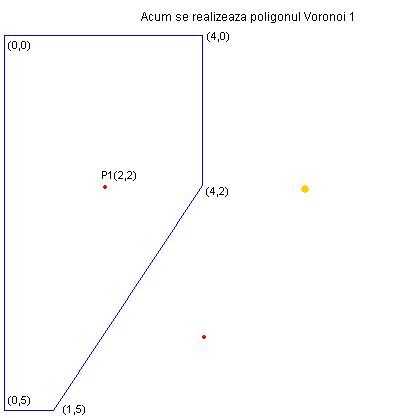
Poligonul 1 are aria 15,5.
Proiect la Analiza algoritmilor
Diagrame
Voronoi
1.Problema diagramelor Voronoi este o frumoasa problema de geometrie computationala care este transpusa in diferite forme . Va prezint in continuare doua enunturi clasice care descriu problema.
1.1.[Diagrama voronoi] Fie cazul de geografie sociala urmator: intr-o tara un
lant de magazine deschide intr-un numar de locatii centre comerciale noi.
Rezolvati problema (de tip calcul de diagrame Voronoi) a asignarii fiecarui
punct geografic din tara la o zona care cuprinde un asemenea nou centru.
Asignarea se face dupa cum pretul produsului principal al lantului de magazine
este minim (pretul unui produs este pretul sau din magazin - egal pentru toate
centrele - plus pretul deplasarii pana la centru, proportional cu distanta in
linie dreapta).
1.2.Postul de televiziune ProInfo are posibilitatea sa-si infiinteze posturi locale in n (1<=n<=200) localitati, ale caror coordonate, specificate relativ la un sistem de coordonate ortogonal cu centrul in coltul stanga jos al unei harti de dimensiuni LxH (1<=L,H<=30000), sunt cunoscute. Cum orice intentie trebuie realizata cu cheltuieli minime, trebuie calculata cu precizie mai buna decat 0.01 puterea minima necesara pentru fiecare statie de emisie, astfel incat sa acopere intreaga zona arondata postului local corespunzator. Mai exact, zona arondata postului local Pi este formata din totalitatea punctelor din planul hartii care sunt mai apropiate de postul local Pi decat de orice alt post, iar puterea necesara statiei de emisie este direct proportionala cu suprafata zonei arondate postului, factorul de proportionalitate fiind egal cu 1 (unu) indiferent de conditiile de relief, clima, etc.
Restrictii de intrare / iesire:
Din fisierul de intrare cu numele INPUT.TXT se citesc:
* de pe prima linie un numar natural n, care reprezinta numarul de posturi;
* de pe urmatoarele n linii, cate o pereche de numere reale, care reprezinta coordonatele localitatilor in care se pot infiinta posturi locale (abscisa si ordonata, separate prin spatiu);
* de pe ultima linie numerele naturale L si H, care reprezinta dimensiunile hartii.
Mentionez ca aceasta problema a fost propusa la barajul pentru lotul olimpic din Timisoara in martie 1997 de Manuela Mateescu si enuntul sau reprezinta datele pe care le-am folosit in implementarea si explicarea Diagramelor Voronoi.
2.1 Datele problemei
Avem la intrare n puncte in planul XOY care sunt posturile locale Pi (1<=i<=n) si pentru care trebuie sa le determinam pe rand "totalitatea punctelor din planul hartii care sunt mai apropiate de postul local Pi decat de orice alt post". Daca analizam problema putin observam ca avem de determinat niste poligoane. Aceste poligoane se numesc Poligoane Voronoi sau Diagrame Voronoi.
2.2 Intelegerea notiunii de Diagrama Voronoi
Ce proprietate au aceste poligoane Voronoi?
Proprietatea lor de baza este ca ele contin toate punctele din "planul hartii care sunt mai apropiate de postul local Pi decat de orice alt post".
Cum putem determina care puncte apartin poligonul Voronoi Pi si care nu?
Ideea rezolvarii problemei consta in determinarea punctelor egal departate intre doua posturi locare, unul fiind cel analizat Pi, iar celalat Pj. Aceste puncte apartine granitei poligoanelor Voronoi ale lui Pi respectiv Pj. Avem asadar o latura comuna celor doua poligoane. Aceasta latura comnuna este un segment de dreapta pe mediatoarea segmentului (Pi,Pj). Avem raspunzul la intrebare:punctele care apartin poligonului Voronoi Pi sunt punctele care sunt de aceeasi parte a mediatoarelor Med(Pi,Pj) ,1<=j<=n si i<>j.
2.3 Algoritmul de rezolvare a Diagamelor Voronoi
Algoritmul parcurge fiecare punct de pe harta care defineste un post local Pi (1<=i<=n). Postului Pi i se atribuie initial ca poligon Voronoi chiar laturile care definesc harta. Initial avem dreptunghiul cu laturile (l,h).
Pasul urmator e de a determina toate mediatoarele laturilor (Pi,Pj) unde 1<=j<=n. Pentru fiecare mediatoare se calculeaza intersectiile cu poligonul Voronoi curent si se pastreaza acea parte din poligonul Voronoi curent care este de aceeasi parte cu mediatoare. Intersectii mediatoarei cu poligonul curent determina noi puncte in nou poligon Voronoi.
In final dupa intersectia cu toate mediatoarele se obtine Diagrama Voronoi al postului Pi. Dupa determinarea poligonului se pot realiza anumite calcule asupra lui. Un exemplu este calcularea arie lui ceea ce duce la rezolvare problemei din enuntul 2.
2.4 Implementarea algoritmului
In continuare va prezint pseudocodul (in mare) a algoritmului descris mai sus.
pentru i=1,n
//se calculeaza poligonul Pi
{poligon(i)=dreptunghiul(l,h); //initial poligonul Voronoi al Pi este
conturul hartii (l,h)
pentru
j=1,n si j<>i
{med(i,j) =calculeaza_mediatoarea_segementului(Pi,Pj);
poligon(i)=
intersecteaza_poligon_cu_mediatoare(poligon(i),med(i,j));
}
afiseaza_poligon;//se poate afisa poligonul
prelucreza_poligon;//sau se poate prelucra pentru
diferite informatii
}
3. Analiza complexitatii algoritmului
Daca privim putin pseudocodul algoritmului observam ca avem doua for-uri imbricate care se ruleaza de n ori. Avem asadar o complxitate O(n*n*complexitate(calculeaza_mediatoarea_segmentului(i,j))*complexitate(intersecteaza _poligon_cu_mediatoare)).
Complexitatea procedurii calculeaza_mediatoarea_segmentului(Pi,Pj) care calculeaza mediatoare med(i,j) o sa vedem ca se executa in timp constant. Avem deci o complexitate O(1).
Complexitatea procedurii intersecteaza _poligon_cu_mediatoare(poligon(i),med(i,j)) se realizeaza printr-un ciclu de dimensiunea poligonului poligon(i) care in cel mai defavorabil caz poate avea dimensiunea 2*n. Rezulta o complexitate O(n).
Complexitatea finala este cubica de O(n^3).
4. Formule matematice folosite in implementarea algoritmului
4.1 Determinarea mediatoarei
Trebuie s determinam analitic coeficientii a,b,c ai dreptei mediatoare. Fie P1(x1,y1) si P2(x2,y2) cele doua puncte care determina mediatoarea. O dreapta poate fii determinata de un punct si o panta. De exemplu: Y-y0=m(X-x0).
Punctul este chiar mijlocul segmentului, care apartine mediatoarei:Pm(xm,ym). xm=(x1+x2)/2 si ym=(y1+y2)/2.
Panta este m=-1/panta(Pi,Pj) deoarece produsul pantelor a doua drepte perpendiculare este -1 (m1*m2=-1). Avem atunci m=-(x1-x2)/(y1-y2), folosind aici definitia pantei a unei drepte determinata de 2 puncte (x1,y1) si (x2,y2) care spune ca md=(y2-y1)/(x2-x1).
Rezulta ca avem urmatoarea ecuatie: Y-ym=-(x1-x2)/(y1-y2)(X-xm) care este echivalenta cu -(x1-x2)/(y1-y2)*X-Y+ym-m*xm=0, de unde putem scoate coeficientii a,b,c stiind ca forma generala a unei drepte este aX+bY+c=0.
Rezulta a=m, b=-1, c=ym-m*xm.
Daca suntem atenti putem observa cazul particular cand y1=y2 si astfel nu mai putem calcula panta cu formula respectiva. Stim totusi ca mediatoarea este determinata de punctul Pm(xm,0) si ecuatia ei trebuie sa descrie o dreapta paralela cu OY(pentru ca segmentul este paralel cu OX si ele sunt perpendiculare intre ele). Asadar ecuatia are forma X=xm care este echivalenta cu -X+xm=0.
Rezulta a=-1, b=0, c=xm.
4.2 Determinarea daca un punct (x,y) este de aceeasi parte cu Pi fata de o dreapta
Acest lucru se determina prin determinarea in ce semiplan se (x,y) fata de dreapta determinata de coeficientii a,b,c. Determinarea semiplanului se afla prin semnul pe care il face punctul fata de dreapta. Daca (x,y) si Pi au acelasi semn atunci sunt in acelasi semiplan determinat de dreapta (a,b,c) si deci sunt in aceeasi parte fata de dreapta.
Formula sign(a*x+b*y+c) intoarce semnul punctului (x,y) fata de dreapta. Daca sign(a*x+b*y+c)=sign(a*Pi(x)+b*Pi(y)+c) atunci cele doua puncte sunt in acelasi seminplan.
4.3 Cum determinam daca un segment intersecteaza o dreapta?
Fie doua puncte P1(x1,y1) si P2(x2,y2) care determina un segment si implicit o dreapta. Daca semnul celor doua puncte fata de dreapta (a,b,c) sunt diferite atunci cele doua puncte sunt in semiplane diferite, de o parte si de alta fata de dreapta (a,b,c), rezulta ca segmentul (P1,P2) intersecteaza dreapta (a,b,c).
Daca (sign(a*x1+b*y1+c)*sign(a*x2+b*y2+c)<0) atunci avem intersectie.
4.4 Cum determinam coefiecientii unei drepte determinate de doua puncte?
Fie doua puncte P1(x1,y1) si P2(x2,y2) care determina dreapta. Avem ecuatia (X-x1)*(y1-y2)=(Y-y1)*(x1-x2) care dupa desfacerea parantezelor si aducerea in aceeasi parte a ecuatiei se ajunge la forma X*(y1-y2)+Y*(x2-x1)+x1*y2-x2*y1.
Avem astfel coefiecientii urmatori: a=y1-y2, b=x2-x1, c=x1*y2-x2*y1.
4.5 Cum determinam punctul P(x,y) de intersectie a segmentului cu dreapta?
Fie doua puncte P1(x1,y1) si P2(x2,y2) care determina un segment si fie dreapta cu coeficientu (a1,b1,c1). Determinam si coeficientii dreptei determinate de punctele P1 si P2 (a2,b2,c2) cu formulele de le 4.4. Urmatorul pas este sa calculam solutia sistemului (a1*x+b1*y+c1=0,a2*x+b2*y+c2=0). Stim ca punctul P(x,y) se afla pe ambele drepte.
Solutia sistemului este: x=(b2*c1-b1*c2)/(a2*b1-a1*b2), y=(a1*c2-a2*c1)/(a2*b1-a1*b2).
5. Exemple
Fie datele de intrare:
n=3 posturi.
P1(x1,y1)=(2,2), P2(x2,y2)=(6,2), P3(x3,y3)=(4,4)
L=10 si H=5
La iesire o sa avem poligoanele ca in imagine cu ariile:15.5; 25,5 si 9.
Poligonul 1 are aria 15,5.

Poligonul 2 are aria 25,5.
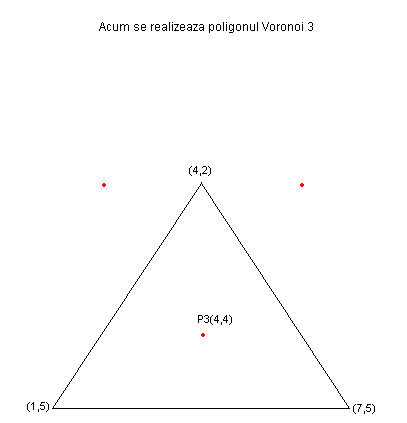
Poligonul 3 are aria 9.
6.Puteti testa cum evolueaza algoritmul in urmatorul applet.